111
Tomek: PLANIMETRIA
| | π | |
jest trójkąt abc. w którym |AC|=|BC| |<acb|=2α > |
| Promień okręgu wpisanego w trójkąt |
| | 2 | |
jest równy r. Wyznacz p[ole ABC... Proszę o pomoc
15 lut 21:45
Tomek: umie ktoś
15 lut 21:54
Tomek: proszę o pomoc
15 lut 22:03
Tomek: up ! proszę chociaż jakaś wskazówka
15 lut 22:18
Godzio:
Uno momento
15 lut 22:23
Godzio:
| | π | |
Sprzeczna treść, <ABC > |
| i |AC| = |BC| |
| | 2 | |
15 lut 22:25
Tomek: nie możliwe, nie abc tylko kąt acb =2α > 90
15 lut 22:30
Tomek: czyli trójkąt będzie równoramienny i będzie kąt rozwarty między tymi ramionami...
15 lut 22:31
Godzio:
aaa coś mi się ubzdurało sorki
już pomagam
15 lut 22:31
Tomek: spoko
15 lut 22:32
Godzio:
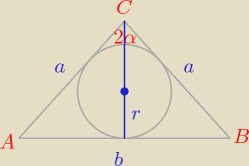
∡C = 2α ⇒ ∡A = ∡B = 90 − α
| | 1 | | 1 | |
P = |
| a2sin2α = |
| r(2a + b) |
| | 2 | | 2 | |
a
2sin2α = r(2a + b)
2asinα = b ⇒ a
2sin2α = r(2a + 2asinα) ⇒ a
2sin2α − a(2r + 2rsinα) = 0
| | 2r − 2rsinα | | 2r(1 − sinα) | |
a(asin2α − 2r + 2rsinα) = 0 ⇒ a = |
| = |
| |
| | sin2α | | sin2α | |
| | 1 | | 1 | 4r2(1 − sinα)2 | |
P = |
| a2sin2α = |
|
| = |
| | 2 | | 2 | sin2α | |
| | 2r2(1 − 2sinα + sin2α) | |
= |
| |
| | sin2α | |
Daj znać czy odpowiedź się zgadza
15 lut 22:42
Tomek: dzięki w piątek wieczorem napisze
(20:00)
15 lut 22:43
Tomek: ale teraz sam to ogarnę
15 lut 22:44
Godzio:
Ok
15 lut 22:45